本發明涉及圖像處理領域，具體地說，特別涉及一種湍流圖像去噪方法。

背景技術：

近年來，國內外學者提出了許多受大氣湍流影響的空中目標去噪算法，提出了一種基于小波閾值湍流圖像去噪方法，該方法基于通用閾值收縮法，實現湍流圖像去噪，該方法的缺點是邊緣過于平滑，算法的收斂速度慢；提出了一種自適應領域的閾值去噪方法(denoisingwaveletthresholdbasedonnabayesshrinkmethod，dwt-nabayesshrink)，該方法基于小波系數特征并結合廣義高斯模型，實現自適應鄰域的閾值去噪，該方法的優點是能夠保留部分圖像細節，但算法計算量大，收斂慢；提出了基于離散小波變換的非線性圖像去噪方法(undecimateddiscretewavelettransform，udwt)，該方法采用非抽樣、位移不變的非正交基小波變換，不同于donoho等提出的正交小波變換，該方法的優點是明顯降低圖像噪聲，很好地保護圖像邊緣信息，但圖像細節信息呈現度不夠。

受成像系統結構及大氣湍流等因素的影響，觀測圖像中含有大量的噪聲，將導致目標圖像畸變十分嚴重，有礙于對空中目標的定位、探測與跟蹤。

技術實現要素：

為了解決現有技術的問題，本發明實施例提供了一種湍流圖像去噪方法。所述技術方案如下：

一方面，提供了一種湍流圖像去噪方法，包括以下步驟：

對含噪湍流圖像進行單層二維離散小波變換，獲得重構的低頻、高頻系數；

提取所述重構的高頻系數，并對所述含噪湍流圖像作快速離散curvelet變換；

根據貝葉斯準則估計閾值t，改進閾值的自適應選取方法，獲得最優閾值，得到去噪的湍流圖像。

可選地，所述對含噪湍流圖像進行單層二維離散小波變換具體為：

采用mallat算法對湍流退化圖像做單層2-d離散小波變換，將其分解為4個子帶，提取分解后的低頻和高頻系數，從系數中重構低頻、高頻系數。

可選地，所述提取所述重構的高頻系數，并對所述含噪湍流圖像作快速離散curvelet變換具體為：

將重構的高頻系數作為輸入，進行基于wrapping的快速離散wdct變換，得到離散的curvelet系數集合c^d(i，j，k)。

可選地，所述將重構的高頻系數作為輸入，進行基于wrapping的快速離散wdct變換，得到離散的curvelet系數集合c^d(i，j，k)的步驟具體如下：

1)對笛卡爾坐標系下的一幅圖像f[t1，t2]進行2-dfft變換，得到2-d頻域表示：

2)對每一對角度、尺度(i，j)，重采樣得到采樣值：

其中，pj為矩形，長度為l1，j，寬度為l2，j；；

3)將采樣得到的與相乘

4)圍繞原點wrap得

其中，經過包裝的窗口數據，由于wd[n1,n2]的限制，被定義為接近原點的一個l1,j×l2,j的矩形內，其中0≤n1＜l1,j，0≤n2＜l2,j；

5)對每個進行2-dfft逆變換，因此得到離散的curvelet系數集合c^d(i,j,k)。

可選地，所述根據貝葉斯準則估計閾值t，改進閾值的自適應選取方法，獲得最優閾值，得到去噪圖像的步驟具體如下：

估計子帶c^d(i，j，k)的最優閾值ti，j；

根據軟閾值函數修整子帶系數c^d(i，j，k)，得到新的高頻系數；

將提取分解后得到的低頻系數和所述新的高頻系數進行wdct逆變換，得到去噪圖像。

可選地，所述估計子帶c^d(i，j，k)的最優閾值ti，j具體為：

根據式估計子帶c^d(i，j，k)的最優閾值ti，j。

可選地，獲取所述式的具體方法如下：

使用軟閾值函數，軟閾值函數δt(x)定義為

式中，t為閾值；

基于貝葉斯估計準則獲得閾值，并與wdct分解的子帶建立關聯；改進chang提出的閾值選取方法，引入尺度參數ξ，則閾值的定義如下

式中，i和j分別表示子帶分解的水平方向和垂直方向，為噪聲信號方差估計，為無噪信號的方差估計；ξ為尺度參數，其定義如下

式中，q為圖像信號分解層數，n是系數c^d(i，j，k)的維度；

對式g(x,y)＝f(x,y)+n(x,y)進行wdct變換，得到

ci,j＝xi,j+vi,j(18)

式中，ci，j表示對觀測圖像g(x，y)變換后的子帶系數，xi，j表示對原圖像f(x，y)變換后的子帶系數，vi，j表示對噪聲n(x，y)變換后的子帶系數；

因為噪聲n(x，y)和原圖像f(x，y)相互獨立，根據式(18)有：

式中，表示觀測圖像方差，表示原圖像方差，噪聲方差是由第一子帶hh1的參數估計的，噪聲方差估計表達式為：

式中，median(|ci,j|)表示給定數值|ci,j|的中值函數，hh1表示第一個子帶；

根據中心極限定理，curvelet變換后的子帶系數ci，j服從廣義高斯分布，其方差的估計為

根據公式(19)和公式(21)，得到的值，為了防止出現負值，修正為

修改式(16)，得到wdct自適應去噪最優閾值估計為

在wdct變換系數不同分解尺度j和不同方向i上選擇自適應最優閾值實現去噪，可提高wdct變換去噪算法的自適應性，獲得更好的去噪效果。

本發明實施例提供的技術方案帶來的有益效果是：

本發明通過提供了一種湍流圖像去噪方法，與dwt-nabayesshrink去噪算法和udwt去噪算法進行比較，通過本方法去噪后的圖像的psnr值提高和mse值明顯降低，并取得良好的視覺效果。

本發明能夠很好地保護圖像細節信息，并且抑制了邊界偽影，視覺效果明顯提高。同時本發明取得了較高的峰值信噪比、較低的均方誤差，有效地去除湍流退化圖像的噪聲。

附圖說明

為了更清楚地說明本發明實施例中的技術方案，下面將對實施例描述中所需要使用的附圖作簡單地介紹，顯而易見地，下面描述中的附圖僅僅是本發明的一些實施例，對于本領域普通技術人員來講，在不付出創造性勞動的前提下，還可以根據這些附圖獲得其他的附圖。

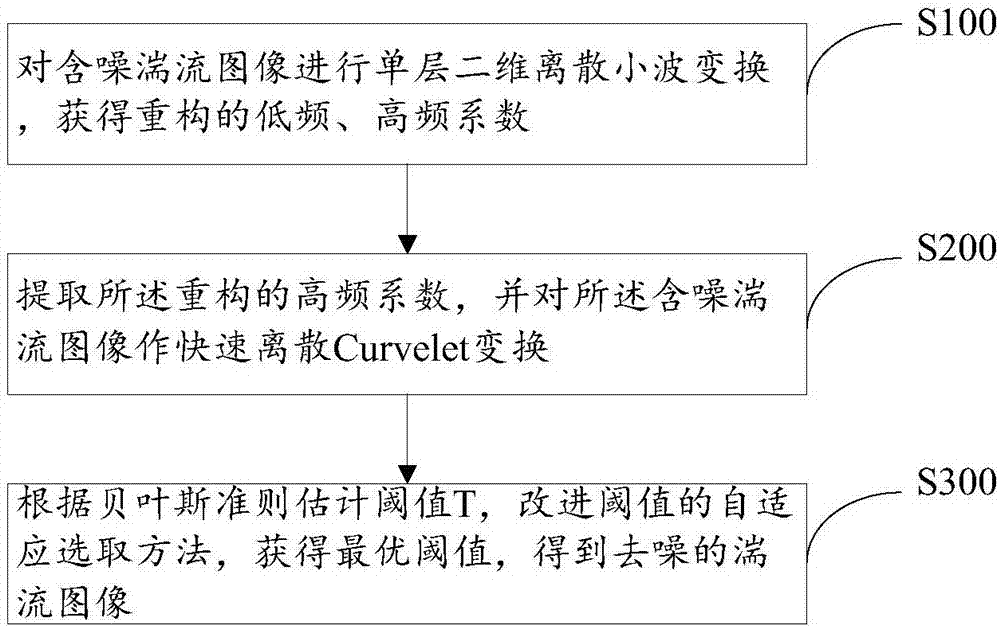
圖1是本發明實施例的一種湍流圖像去噪方法流程圖。

具體實施方式

為使本發明的目的、技術方案和優點更加清楚，下面將結合附圖對本發明實施方式作進一步地詳細描述。

本發明提供了一種湍流圖像去噪方法，參見圖1，包括以下步驟：

s100：對含噪湍流圖像進行單層二維離散小波變換，獲得重構的低頻、高頻系數；

具體地，所述對含噪湍流圖像進行單層二維離散小波變換，獲得重構的低頻、高頻系數具體為：

采用mallat算法對湍流退化圖像做單層2-d離散小波變換，將其分解為4個子帶，提取分解后的低頻和高頻系數，從系數中重構低頻、高頻系數。

s200：提取所述重構的高頻系數，并對所述含噪湍流圖像作快速離散curvelet變換；；

具體地，所述提取所述重構的高頻系數，并對所述含噪湍流圖像作快速離散curvelet變換具體為：

將重構的高頻系數作為輸入，進行基于wrapping的快速離散wdct變換，得到離散的curvelet系數集合c^d(i，j，k)。

s300：根據貝葉斯準則估計閾值t，改進閾值的自適應選取方法，獲得最優閾值，得到去噪的湍流圖像。

具體地，所述根據貝葉斯準則估計閾值t，改進閾值的自適應選取方法，獲得最優閾值，得到去噪圖像的步驟具體如下：

估計子帶c^d(i，j，k)的最優閾值ti，j；

根據軟閾值函數修整子帶系數cd(i，j，k)，得到新的高頻系數；

將提取分解后得到的低頻系數和所述新的高頻系數進行wdct逆變換，得到去噪圖像。

本實施例中，本發明的基本思路是：首先采用二維離散小波變換(2-ddiscretewavelettransform，2-ddwt)方法將湍流退化圖像分解為4個子帶，然后對高頻系數進行基于wrapping的快速離散curvelet變換，再基于貝葉斯估計準則改進閾值選取方法，以修整curvelet子帶系數，實現湍流退化圖像的去噪目的。

具體地，本發明一種湍流圖像去噪方法還提供了wdct的原理，具體如下：

湍流圖像的退化模型為：

g(x,y)＝f(x,y)+n(x,y)(1)

其中，g(x，y)是觀測的湍流退化圖像，f(x，y)是原圖像，h(x，y)是點擴散函數，n(x，y)為高斯噪聲，圖像的空間坐標(x，y)∈ω，ω是圖像域。

對于給定的圖像函數f(x)∈l²(r²)，連續curvelet變換采用基函數與圖像信號f(x)的內積形式實現圖像信號的稀疏表示，則圖像f的curvelet變換表示為

式中，是curvelet基函數，i，j，k分別是方向，尺度和位置變量。根據plancherel定理，在頻域的圖像離散的curvelet變換為

本文采用基于wrapping算法的快速離散curvelet變換，因為這是目前所能實現的最快的離散curvelet變換^[15]。在笛卡爾坐標系，設f[t1，t2](0≤t1,t2＜n)表示一幅圖像，對公式(3)做基于wdct變換，得到子帶系數c^d(i，j，k)

式中，上標d表示離散，每個是離散的curvelet波形。為了實現離散化，用同中心的方形代替同中心的圓形^[16]。在笛卡爾坐標系，設ω為頻域變量，γ和θ為頻域的極坐標，重新定義射線窗口(wj)j≥0，wj(ω)＝w(2^-jω)，這些窗口的形式為

式中，φ是一維低通窗口的積，其計算公式為：

φj(ω1,ω2)＝φ(2^-jω1)φ(2^-jω2)(6)

其中，函數滿足0≤φ≤1，在[-0.5，0.5]區間，可能等于1，在-[2，2]之外消失，由此可得

在笛卡爾坐標系，角度窗口vj為

因此，我們使用和vj定義“笛卡爾”局部窗函數

引入一組等間隔斜率定義為

其中，剪切矩陣為的區間是受w和v區間限制的楔形區域，該楔形區域為{(ω1,ω2):2^j≤ω1≤2^j+1,-2^-j/2≤ω1/ω2≤2^-j/2}。

具體地，本實施例中，基于wrapping算法的wdct變換具體實現步驟如算法1。

算法1，基于wrapping算法的wdct變換步驟如下：

step1:對笛卡爾坐標系下的一幅圖像f[t1，t2]進行2-dfft變換，得到2-d頻域表示

step2:對每一對角度、尺度(i，j)，重采樣得到采樣值

其中，pj為矩形，長度為l1，j，寬度為l2，j。

step3：將采樣得到的與相乘

step4：圍繞原點wrap得

其中，經過包裝(wrapped)的窗口數據，由于wd[n1,n2]的限制，被定義為接近原點的一個l1,j×l2,j的矩形內，其中0≤n1＜l1,j，0≤n2＜l2,j。

step5：對每個進行2-dfft逆變換，因此得到離散的curvelet系數集合c^d(i,j,k)。

本實施例中，還提供了閾值計算的方法，在wdct算法中，選擇閾值函數和閾值是至關重要的。常用的閾值處理函數有硬閾值函數和軟閾值函數，本實施例中使用軟閾值函數。軟閾值函數δt(x)定義為

式中，t為閾值。

本發明基于貝葉斯估計準則獲得閾值，并與wdct分解的子帶建立關聯。改進chang提出的閾值選取方法，引入尺度參數ξ，則閾值的定義如下

式中，i和j分別表示子帶分解的水平方向和垂直方向，為噪聲信號方差估計，為無噪信號的方差估計。ξ為尺度參數，其定義如下

式中，q為圖像信號分解層數，n是系數c^d(i，j，k)的維度。

對式(1)進行wdct變換，得到

ci,j＝xi,j+vi,j(18)

式中，ci，j表示對觀測圖像g(x，y)變換后的子帶系數，xi，j表示對原圖像f(x，y)變換后的子帶系數，vi，j表示對噪聲n(x，y)變換后的子帶系數。

因為噪聲n(x，y)和原圖像f(x，y)相互獨立，根據式(18)有：

式中，表示觀測圖像方差，表示原圖像方差，噪聲方差是由第一子帶hh1的參數估計的，噪聲方差估計表達式為：

式中，median(|ci,j|)表示給定數值|ci,j|的中值函數，hh1表示第一個子帶。

根據中心極限定理，curvelet變換后的子帶系數ci，j服從廣義高斯分布，其方差的估計為

根據公式(19)和公式(21)，得到的值，為了防止出現負值，修正為

修改式(16)，得到wdct自適應去噪最優閾值估計為

在wdct變換系數不同分解尺度j和不同方向i上選擇自適應最優閾值實現去噪，可提高wdct變換去噪算法的自適應性，獲得更好的去噪效果。

具體地，本實施例中，提出的湍流圖像去噪算法實現的具體步驟如算法2，即：

step1：采用mallat算法對湍流退化圖像做單層2-d離散小波變換，將其分解為4個子帶，提取分解后的低頻和高頻系數，從系數中重構低頻、高頻系數；

step2：根據實施例中的算法1，將重構的高頻系數作為輸入，進行基于wrapping的快速離散wdct變換，得到curvelet系數c^d(i，j，k)；

step3：根據式(23)估計子帶c^d(i，j，k)的最優閾值ti，j；

step4：根據軟閾值函數修整子帶系數c^d(i，j，k)，得到新的高頻系數；

step5：將step1得到的低頻系數和step4得到的高頻系數進行wdct逆變換，得到去噪圖像。

本發明實施例提供的技術方案帶來的有益效果是：

本發明通過提供了一種湍流圖像去噪方法，與dwt-nabayesshrink去噪算法和udwt去噪算法進行比較，通過本方法去噪后的圖像的psnr值提高和mse值明顯降低，并取得良好的視覺效果。

本發明能夠很好地保護圖像細節信息，并且抑制了邊界偽影，視覺效果明顯提高。同時本發明取得了較高的峰值信噪比、較低的均方誤差，有效地去除湍流退化圖像的噪聲。

以上僅為本發明的較佳實施例，并不用以限制本發明，凡在本發明的精神和原則之內，所作的任何修改、等同替換、改進等，均應包含在本發明的保護范圍之內。