本發明涉及目標識別、圖像分割、遙感、醫學圖像分析等領域。

背景技術：

邊緣信息是圖像中極其重要的信息，理論上，通過邊緣信息可恢復圖像中的全部信息。因而邊緣檢測是圖像分析的重要內容；是處理許多問題的關鍵；傳統的邊緣檢測主要是運用水平方向和垂直方向的差分算子分別檢測出水平方向和垂直方向的邊緣，然后合成某種梯度進行邊緣檢測，計算機實現時只需求出兩個方向的差分，然后合成即可，但這種方法也有明顯的不足，它們只強調水平、垂直，兩個方向的邊緣信息，但一般實際圖像中包含有多個方向甚至是任意方向的邊緣信息。

數學形態學是分析圖像幾何特征的有力工具，它通過運用一些基本的集合運算，如腐蝕、膨脹、開、閉等對圖像形狀和結構進行分析處理，在諸如圖像增強的圖像處理中得到了很好的應用，形態學中腐蝕、膨脹運算的形態學梯度具有較好的圖像邊緣檢測效果，但是腐蝕和膨脹的運算都是極值運算，因而僅有腐蝕、膨脹會對圖像梯度信息產生不可避免的影響。

技術實現要素：

針對上述不足，本發明提出了一種新的圖像邊緣提取方法。

本發明的目的是：提取圖像邊緣，使提取到的邊緣具有更加豐富的細節信息，更具完整性、連續性、多方向性。

本發明為實現上述目的所采用的的技術方案是：一種圖像邊緣提取方法，該方法的實施步驟如下：

步驟1：用低通濾波器H₀對原圖像做不可分加性小波多尺度分解，得到一個低頻子圖和多層高頻子圖像。

步驟2：利用形態學梯度算子對第一步中分解出的低頻子圖像進行形態學梯度濾波得到濾波梯度圖。

步驟3：對步驟一中得到的多層高頻子圖像相加，得到增強了邊緣信息的高頻子圖像，對高頻子圖像取小波變換的模極大值，得到一個高頻子圖像，即邊緣 圖。

步驟4：將梯度圖1和邊緣圖像2做加性小波逆變換(相加)，得到結果梯度圖。

步驟5：對第4步得到的梯度圖進行二值化，得到初步邊緣圖。

步驟6：利用形態學中除去孤立點、去毛刺以及去H型點和邊緣單一化等操作，得到結果邊緣圖。

本發明的有益效果是：本方法操作簡單、檢測效果好；它能檢測出圖像中灰度值變化較小的目標，獲得更多的邊緣細節，能提取具有完整性、多方向性、連續和平移不變性的邊緣。與其他的檢測方法相比，本方法還具有有較快的處理速度。

附圖說明

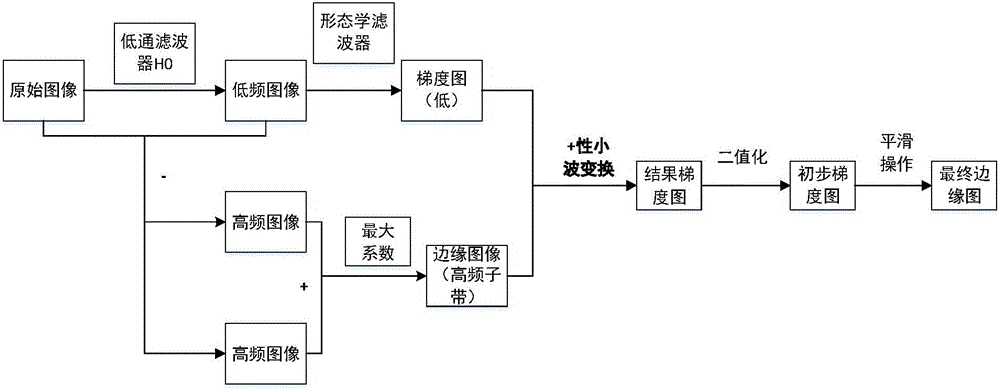
附圖是本發明的流程圖

具體實施方式

本方法構造了一個二維不可分低通濾波器；先對原圖像做多尺度不可分加性小波分解，然后利用現代數學形態學梯度算子獲取分解后的子圖像的梯度圖，高頻子圖像相加從而分別提取低、高頻子圖像的邊緣,然后重形成最終的邊緣圖像，并利用此二維不可分加性小波各向同性和形態學梯度檢測邊緣的豐富、快速等特點，提出了一種新的圖像邊緣提取方法。

以下結合流程圖，對本發明進行詳細說明。

一、低通濾波器H₀

由于不可分加性小波有很好的方向性,是各相同性的，為了獲得多方向的圖像邊緣信息，本發明選用6*6的不可分低通濾波器，其構造方法如下：

首先，將伸縮矩陣為[2，0；0，0]的，具有緊支撐、對成性、正交性的6*6的濾波器組表示為：

(H₀(x，y)，H₁(x，y)，H₂(x，y)，H₃(x，y))＝T (1)

其中，U_j(j＝1，2，...，K)為中心對稱正交陣，w_i為小波平面，D(x，y)＝Diag(1，x，y，xy)，V＝(V₀，V₁，V₂，V₃)為正交陣，V₁，V₂，V₃ 為4×1向量，V₀＝(1，1，1，1)^T。

當選取K＝2時候，構造：

式(1)至式(6)是濾波器，原始圖像經過濾波器后得到一個低頻子圖和多層高頻子圖像。

二、形態學梯度算子

步驟二中，采用形態學梯度算子對低頻子圖像進行形態學梯度濾波，得到濾波梯度圖，其中形態學梯度是數學形態學中由結構元素來描述圖像鄰域內灰度值變化情況的一種梯度，在灰度值形態學中,最基本的腐蝕、膨脹運算分別是非擴展變換和擴展變換,由此可以產生以下梯度。

在本方法中，主要構造以下幾種基本形態梯度：

1)膨脹類型：

2)腐蝕型：T₂＝f-fΘb

3)開操作型：

4)閉操作型：

其中，表示膨脹操作，Θ表示腐蝕操作，○表示開運算操作，●表示閉運算操作。

腐蝕、膨脹、開、閉等操作按一定的合理順序組合可形成多種形式的數學形 態學梯度，在本方法中圖像邊緣檢測中選擇的形態學梯度為：

即先對原圖像進行閉操作運算,然后對結果分別進行膨脹運算和開運算，最后求兩者的差得形態學梯度圖。

膨脹和腐蝕是兩種最基本的形態學運算，其他的運算時這兩種運算的組合，因而這種組合是圖像中在結構元素所限定的范圍內的最大值、最小值按一定順序的組合，而形態學梯度是兩種這樣的組合所得到的值的差，而只要結構元素所在區域的灰度值不全相同，則必有最大值和最小值。本文在本方法中，選擇的最大值、最小值的組合運算方式分別為：最大值(最小值(最大值))和最大值(最小值(最小值(最大值)))(括號按從內到外的順序運算)，其選擇的形態學梯度為上兩種組合方式的差，即T＝最大值(最小值(最大值))-最大值(最小值(最小值(最大值)))。

顯然，對于任意大小的結構元素窗口，上述表達式的均值大于0，因此，它完全可以作為梯度算子，而且，只有當結構元素所在區域作第一次膨脹運算的所得結果為相同的灰度值時，上述表達式的值才為0，其它情況下的值都大于0，因而能很好地檢測出圖像中的變化。

四、最終邊緣圖像的獲得

原始圖像經過濾波器，得到的多層高頻子圖像，將得到的多層高頻子圖像相加，此時得到增強了邊緣信息的高頻子圖像，對高頻子圖像取小波變換的模極大值，得到一個高頻子圖像，即邊緣圖。將梯度圖和邊緣圖像做加性小波逆變換(相加)，得到結果梯度圖。然后對得到的結果梯度圖進行二值化，得到初步邊緣圖。最后，利用形態學中除去孤立點、去毛刺以及去H型點和邊緣單一化等操作，得到結果邊緣圖。